第6章 決済の準備3.クリアリングの性質
受取と支払とが溶け込んでいる
クリアリング・ハウスが行うネッティングには固有の難しい問題があります。それは、クリアリング・ハウスが各銀行について算出した「勝ち額」や「負け額」には、それぞれの銀行の全ての受取と支払が「溶け込んでいる」ということです。
例えば今日、あるクリアリング・ハウスに持ち込まれたたくさんの振替指示書のうち、A銀行関係のものを取りだしてみたら、A銀行はよその銀行100行から合計100億円を受け取る一方、よその銀行に101億円支払うようになっていたとします。予定される受取総額は100億円、支払総額は101億円ですから、A銀行は今日「負け銀行」となっていて、「負け額」は1億円です。この「負け額1億円」という数字の中には、100億円の受取と101億円の支払とが混ざり合って隠れているのです。
| 受取 | 支払 | |
|---|---|---|
| B銀行から | 30 | |
| B銀行から | 10 | |
| B銀行へ | 51 | |
| C銀行から | 20 | |
| C銀行から | 40 | |
| D銀行へ | 30 | |
| E銀行へ | 20 | |
| 合計 | 100 | 101 |
| 差引き | 支払 1 | |
さて、いまA銀行が何かの事情(倒産とかコンピューターの故障など)で、この負け額1億円を決済できなくなったとします。この場合、「受取が100億円あるのだから、支払101億円のうち100億円は決済できるのではないか」と思われるかもしれません。
しかし、クリアリング・ハウスというのは、「受払いを差引きして、効率的な決済を行おう」とする仕組みであり、多くの場合「差額を決済できたら、クリアリングする前に存在した全ての受取と支払が決済できたことにしよう」という作りになっています。このため、そもそもA銀行には100億円というお金が実際には入ってこないわけで、「入ってきた」100億円を使って100億円分の支払を行う、などということはできません。「負け額」が払えないと、全ての支払と受取が出来なかったことになってしまうのです。
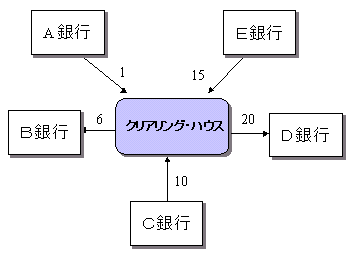
| A銀行 | -1 |
|---|---|
| B銀行 | 6 |
| C銀行 | -10 |
| D銀行 | 20 |
| E銀行 | -15 |
| 合計 | 0 |
各銀行の決済が関係しあっている
さらに、すでにお話ししたように、「負け銀行の負け額の合計=勝ち銀行の勝ち額の合計」です。すべての負け銀行は、負け額をクリアリング・ハウスに支払い、クリアリング・ハウスは、このおかねを勝ち銀行たちに払い出します。そのため、負け銀行が1行でも負け額を支払えないと、クリアリング・ハウスは勝ち銀行たちに払い出すおかねが不足してしまいます。
もちろん、その他の負け銀行が支払ってくれたおかねを使って、一部の勝ち銀行には払い出せるかもしれません。しかし、その他の勝ち銀行はおかねが受取れなくなって、損をすることになります。したがって、どの勝ち銀行もクリアリング・ハウスに対し「自分には払い出せ」と要求するはずですから、払い出すおかねが全額手元に揃っていないクリアリング・ハウスとしては、結局のところ、どの勝ち銀行にも払い出せなくなってしまいます。こういうことでは、誰も安心してこのクリアリング・ハウスを利用しないでしょう。
以上からお分かりのように、銀行同士が1件1件の取引をバラバラに決済するのと違って、クリアリングあるいはネッティングは、全ての取引を他の全ての取引と関係させてしまうのです。ある銀行の受取と支払が「溶け込んで」しまうだけでなく、どこか1行でも決済できない銀行が現れると他の全ての銀行の決済も出来なくなってしまいます。これはクリアリングのもつ最も重要な特徴です。