このページの本文へ移動

わが国の自然利子率の決定要因―DSGEモデルとOGモデルによる接近― 須藤直、岡崎陽介、瀧塚寧孝（日本銀行）

Research LAB No.18-J-2, 2018年6月13日

キーワード：
自然利子率、DSGEモデル、OGモデル

JEL分類番号：
E20、E32、E43、E44、E52、J11

Contact:
nao.sudou@boj.or.jp（須藤）

要旨

自然利子率は、直接観察できないため、様々な手法による推計を基に総合的に判断することが必要である。本稿は、構造型アプローチを用いて自然利子率を分析した岡崎・須藤（2018） [PDF 1,122KB]と須藤・瀧塚（2018） [PDF 1,218KB]の結果を基に、自然利子率の動向や変動要因、先行きの自然利子率への人口動態要因の影響について整理する。

これら構造型アプローチおよび他の手法によるそれぞれ異なる推計結果を総合的に判断すると、わが国の自然利子率は、1990年代から趨勢的に低下し、最近は概ね0%程度の範囲内にあるとみられる。構造型アプローチによれば、こうした変動の主因は技術進歩率の変化であり、金融仲介活動の機能度の変化も時期により相応に寄与している。先行きの自然利子率は、これらの要因の帰趨に依存する可能性が高い。少子高齢化による人口動態要因は、先行き自然利子率の下押しに働くものの、その水準をはっきりと押し下げるものではないとみられる。

はじめに

自然利子率とは、経済・物価に対して引き締め的にも緩和的にも作用しない中立的な実質金利の水準のことである。自然利子率は、中央銀行にとっては金融政策スタンスが引き締め的か緩和的かを判断する際のベンチマークの一つとなることから、理念的には、これを推計し、現実の実質金利の動向を自然利子率との相対的な関係で捉えていくことが重要である。実際、海外の主要中央銀行の幹部からは、しばしば自然利子率への言及がみられる（Carney [2016]、Constancio [2016]、Yellen [2016]）。もっとも、自然利子率は、直接的には観察できないものであり、また推計手法についてのコンセンサスも確立しておらず、特定の手法に基づいて推計された結果のみを基にその水準を測ることは適当ではない。このため、異なる複数の手法を用いて推計したうえで、各手法に共通して現れる傾向からその水準と推移を総合的に判断するアプローチが必要となる。この際、各推計手法間には優劣がないことに加え、各手法による推計値について幅を持ってみなければならないことに留意することも重要である。

日本銀行では、2016年に実施した「総括的な検証」の中で、幾つかの手法を用いてわが国の自然利子率を推計したが（日本銀行[2016]、岩崎ほか[2016]）、今回、これらを補完するものとして、ニューケインジアン型動学的確率的一般均衡モデル（Dynamic Stochastic General Equilibrium Model、DSGEモデル）および世代重複モデル（Overlapping Generations Model、OGモデル）を用いて、自然利子率を推計した。これら2つの手法は、自然利子率変動の背景・要因を確認することができる構造型アプローチであり、海外の主要中央銀行などでも利用が増えている手法である（Del Negro et al. [2017]、Gagnon et al. [2016]、Gerali and Neri [2017]、Goldby et al. [2015]）。構造型アプローチでは、自然利子率に作用する家計・企業部門の経済行動について、これに影響を与える技術進歩率や人口動態、金融仲介活動の機能度といった経済構造も含めてモデル化したうえで、これら経済構造の変化と自然利子率を結び付けて分析する。これにより、自然利子率の変動要因の特定や、今後の経済構造の変化が自然利子率に与える影響などの検証が可能になる1。

  1. もっとも、構造型アプローチの推計値は、「総括的な検証」で用いた手法による推計値と比べて、モデルの定式化に依存する傾向が強い。

DSGEモデルでみた自然利子率の決定要因

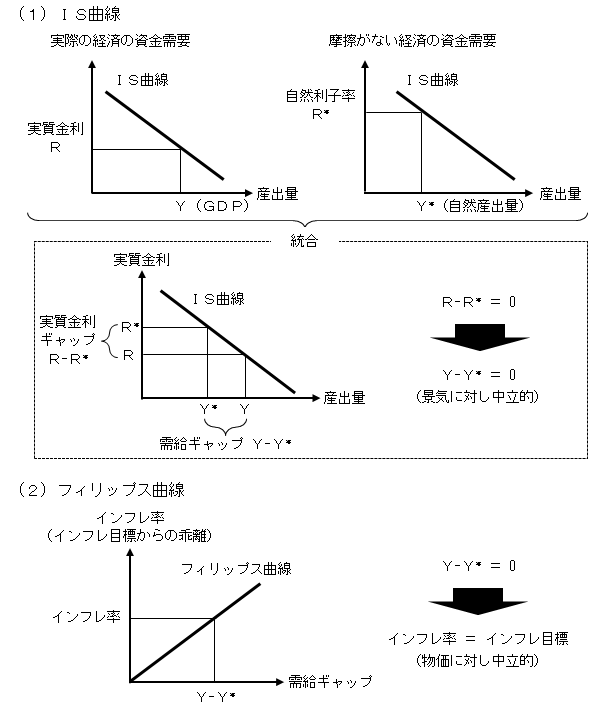
ニューケインジアン型DSGEモデルとは、各国中央銀行や学界などで広く用いられているマクロモデルである。この枠組みでは、経済が自然産出量から乖離し得る原因を、名目硬直性に由来する摩擦に求めている。そのもとで自然利子率は、名目硬直性が存在せず、自然産出量が常に達成されるような仮想的な経済における実質金利として定式化される2。図1が示すように、実質金利ギャップと需給ギャップの負の関係を表すIS曲線を前提とすると、現実の実質金利と自然利子率の水準が一致すれば、GDPは自然産出量と一致する。このように需給ギャップがゼロであれば、需給ギャップとインフレ率の正の関係を表すフィリップス曲線を前提とすると、インフレ率は目標値と一致する。この意味で、自然利子率は冒頭で述べた定義通り、経済・物価に対して中立的な実質金利となる。

図1. ニューケインジアン型モデルにおける自然利子率の性質

  • IS曲線上で、現実の実質金利と自然利子率の水準が一致すれば、GDPは自然産出量と一致することを示した図。需給ギャップがゼロであれば、フィリップス曲線上でインフレ率は目標値と一致することを示した図。

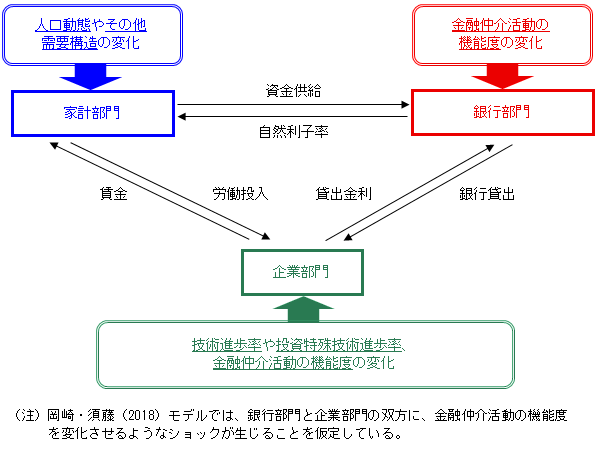
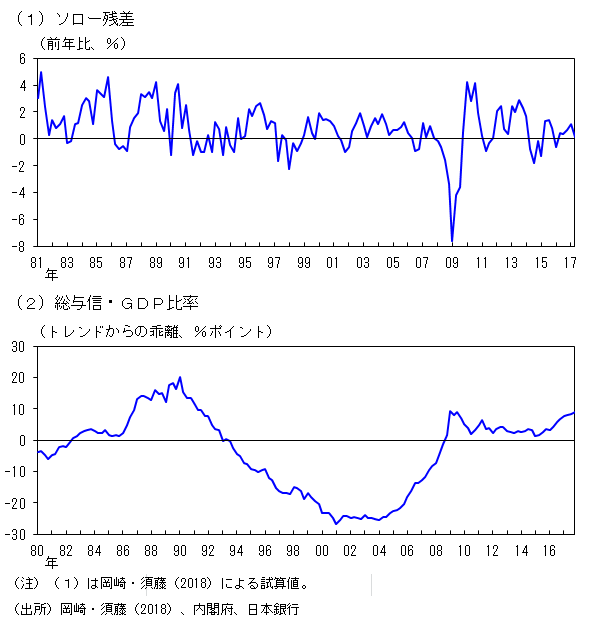
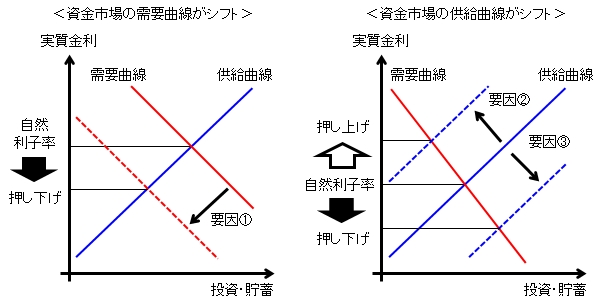
自然利子率は、摩擦がない経済における実質金利であり、資金市場における需要・供給曲線の交点で定まる。岡崎・須藤（2018）では、こうした需要・供給曲線をシフトさせ得る経済構造の変化として、Rachel and Smith (2015)やSummers (2014)などの先行研究で重要とされている5つの要因に注目し、これらと自然利子率の関係性を組み込んだモデルを日本のデータを用いて推計することで、各要因の寄与を定量的に評価している。具体的に5つの経済構造とは、（i）全産業横断的な技術進歩率（以下、技術進歩率）、（ii）金融仲介活動の機能度、（iii）人口動態3、（iv）投資財部門固有の技術進歩率（以下、投資特殊技術進歩率）、（v）その他需要構造である。それぞれの変化は、資金需要量や資金供給量を変化させ、自然利子率を変動させる（図2）。特に、わが国では、技術進歩率の代理変数であるソロー残差の伸び率が、1990年代初め頃から低迷していることが広く知られており（図3（1））、技術進歩率の低下に起因する資本収益率の低下が、企業部門の投資需要を減退させ、自然利子率を押し下げた可能性が考えられる。また、1990年代半ば以降に発生した銀行危機では、企業・銀行部門のバランスシートの毀損を契機とした信用量の収縮がみられたことを踏まえると（図3（2））、金融仲介活動の機能度の低下も、企業・銀行部門の資金需要の低下を通じて、自然利子率を押し下げた可能性がある。

図2. 岡崎・須藤（2018）モデルにおける資金の流れ

  • 岡崎・須藤モデルの概要。人口動態やその他需要構造の変化が家計部門に影響を与え、金融仲介活動の機能度の変化が銀行部門に影響を与え、技術進歩率や投資特殊技術進歩率、金融仲介活動の機能度の変化が企業部門に影響を与える。

図3. 技術進歩率と総与信・GDP比率

  • (1)ソロー残差、(2)総与信・GDP比率の時系列グラフ。詳細は本文のとおり。

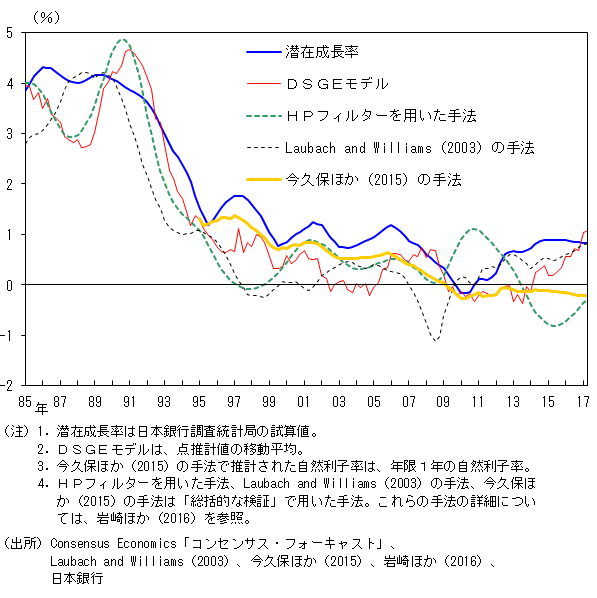
図4では、DSGEモデルで推計された自然利子率と「総括的な検証」で用いた手法により推計された自然利子率を示している。何れの推計値も、1990年代から趨勢的に低下し、2000年代以降0～1%程度の水準で推移している点は共通している。最近数年については、DSGEモデルやLaubach and Williams (2003)の手法を用いた推計値が0%台後半まで上昇してきている潜在成長率に向けて上向いてきている一方、今久保ほか（2015）の手法やHPフィルターを用いた推計値は、若干のマイナスないしマイナス幅を拡大する方向で推移している。このように推計手法によって、推計値には相応の幅があるが、これらを踏まえて総合的に判断すると、最近の自然利子率は、概ね0%程度の範囲内で推移していると考えられる。

図4. 様々な手法による自然利子率

  • 潜在成長率、DSGEモデル、HPフィルターを用いた手法、Laubach and Williams (2003)の手法、今久保ほか（2015）の手法の時系列グラフ。詳細は本文のとおり。

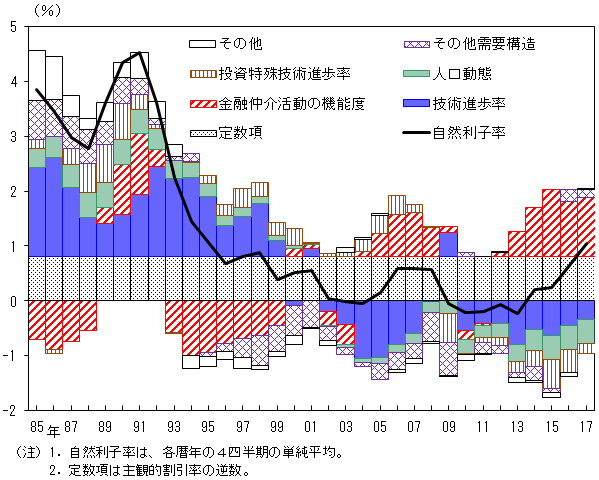
図5は、DSGEモデルを用いた自然利子率について、その変動をもたらした経済構造について要因分解したものである。図から明らかなように、この間の自然利子率の変動における最大の要因は、技術進歩率である。例えば、1980年代から直近までの自然利子率の低下幅約4%ポイントのうち、2%ポイント強が技術進歩率の変化に起因する。次に重要な要因は、金融仲介活動の機能度である。ただしこの要因は、自然利子率を趨勢的に押し下げるのでなく、押し上げにも作用している。例えば、わが国で銀行危機が発生した1990年代半ばから2000年代前半にかけては、自然利子率を1%ポイント近く押し下げた一方、最近は押し上げ要因となっている。この2つの要因に比べると、他の要因の影響は限定的である。

図5. DSGEモデルを用いた自然利子率の要因分解

  • DSGEモデルを用いた自然利子率について、その変動をもたらした経済構造について要因分解したグラフ。詳細は本文のとおり。
  1. 2厳密には、名目硬直性が存在せず、フィリップス曲線へのショックがない経済を想定している。詳細については、例えば、Woodford (2003)を参照されたい。
  2. 3岡崎・須藤（2018）では、人口動態のうち、生産年齢人口の変化のみを分析しているのに対し、須藤・瀧塚（2018）では、寿命の変化も分析している。

OGモデルでみた先行きの自然利子率への人口動態要因の影響

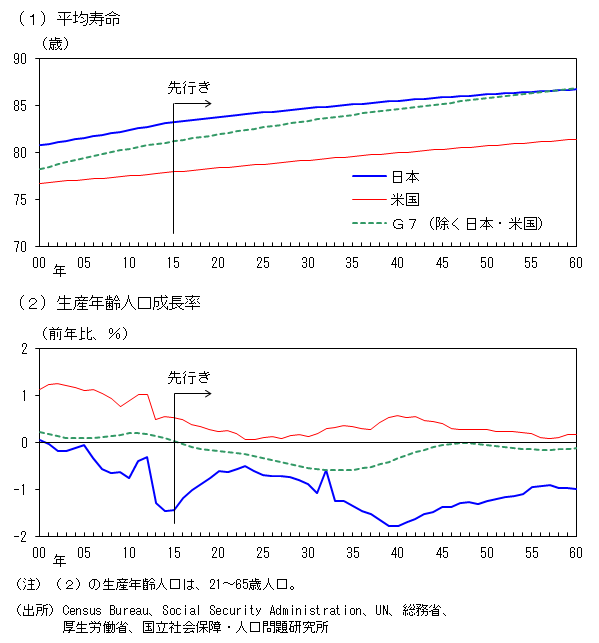
先行きの自然利子率も、技術進歩率や金融仲介活動の機能度をはじめとする経済構造の変化に大きく依存して推移する可能性が高い。これら経済構造の先行きを予測することは容易ではないが、経済構造のうち人口動態については、相対的に予見しやすいと考えられる。わが国の場合、他国と比べて顕著な少子高齢化が今後も進展していくことが確実視されており（図6）、こうした人口動態要因が先行きの自然利子率に及ぼす影響を評価しておく意義は大きい。

図6. 少子高齢化の先行きに関する国際比較

  • (1)平均寿命、(2)生産年齢人口成長率の日本と米国とG7(除く日本・米国)の時系列グラフ。詳細は本文のとおり。

そこで、以下では、OGモデルを用いた自然利子率のシミュレーション結果を紹介する。OGモデルとは、家計の経済行動が年齢ごとに異なることに着目して、年齢が異なる複数の世代を明示的にモデル化したものであり、人口動態の変化とマクロ経済変数の関係性について含意を有することから、社会保障制度の分析などに広く用いられる。ここで紹介する須藤・瀧塚（2018）のモデルは、わが国の家計のライフサイクルをできるだけ再現する形でモデル化された80世代からなる家計部門と、わが国の実際の制度と整合的となるようにモデル化された社会保障部門、政府部門から構成されており、経済全体の人口分布の変化が、自然利子率に与える影響について詳細に分析することができると考えられる。とりわけ、少子高齢化の自然利子率への影響は、理論的には押し上げと押し下げ双方があり得るため（図7）、ネットでみた評価については、こうした精緻なモデルを用いることが必要になる。

図7. 少子高齢化が自然利子率に与える影響

図7. 少子高齢化が自然利子率に与える影響
要因 資金市場への影響 自然利子率への影響
1. 労働投入量の低下 資本ストックが相対的に過剰になるため、資金需要が減少 押し下げ
2. 高齢者の貯蓄取り崩し 貯蓄取り崩し主体が増加することから、資金供給が減少 押し上げ
3. 長寿化に備えた家計の貯蓄増加 長寿化により、平均寿命が長くなることから、先を見据えた貯蓄が増加し、資金供給が増大 押し下げ
  • 需要・供給曲線を用いた図。資金需要が減少した場合、自然利子率が低下。資金供給が減少した場合、自然利子率が上昇。資金供給が増大した場合、自然利子率が低下。

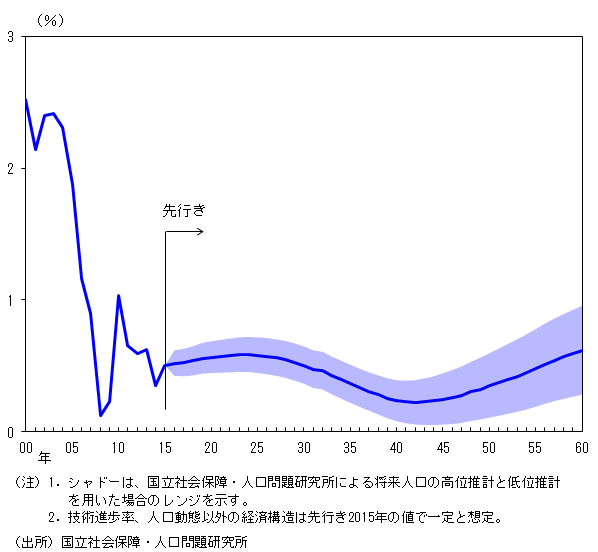
図8は、国立社会保障・人口問題研究所による人口動態予測を用いて、先行き2060年までの自然利子率の推移を計算したものである4。ここで、技術進歩率などの経済構造については、直近と同水準で推移するとの想定を置いている。これによれば自然利子率は、今後、2040年代にかけてごく緩やかに低下するものの、0%以下まで落ち込むことはなく、長い目でみれば近年と概ね同水準で推移する。

図8. OGモデルによる先行きの自然利子率のシミュレーション

  • グラフ：国立社会保障・人口問題研究所による人口動態予測を用いて、先行き2060年までの自然利子率の推移を計算したもの。詳細は本文のとおり。

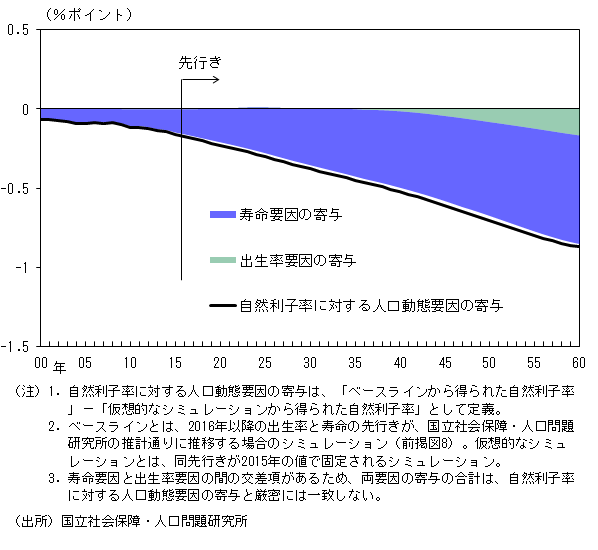
こうした自然利子率の推移に関して、今後の少子高齢化の進行が如何に作用しているかを明らかにするため、前述の人口問題研究所の推計値に沿って少子高齢化が進展した場合（ベースライン）に加え、出生率と寿命の先行きが2015年時点の値から不変であった場合（仮想的なシミュレーション）についても自然利子率を計算し5、両者の乖離を要因分解したものが図9である。ここからは、人口動態要因はネットでみて自然利子率を押し下げる方向に寄与していること、また、押し下げ寄与の主因は、寿命要因であることが確認できる。これは、長寿化を予想した家計が将来に備えて貯蓄を増加させることで、マクロ経済全体でみた資本ストック量が労働供給量対比で過剰になり、自然利子率が低下するというメカニズムが働いた結果であると考えられる。

図9. 自然利子率に対する人口動態要因の寄与

  • グラフ：自然利子率に対する人口動態要因の寄与（寿命要因、出生率要因）。詳細は本文のとおり。

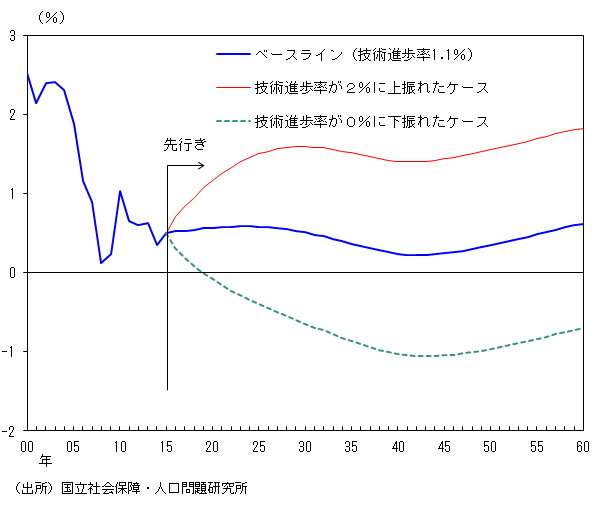
もちろん、実際の先行きの自然利子率の動向は、このシミュレーションで一定とした人口動態以外の経済構造の変化にも大きく依存することに改めて留意する必要がある。例えば、技術進歩率の先行きが、図9のシミュレーションで用いた直近時点の値の1.1%から2%に上振れたケースと、逆に0%へ下振れたケースについてシミュレーションを行うと、前者では自然利子率が2%近くまで上昇する一方、後者では自然利子率が明確なマイナスで推移するなど、結果は顕著に変化する（図10）。

図10. 技術進歩率が上振れたケースと下振れたケースの自然利子率

  • グラフ：技術進歩率が上振れたケースと下振れたケースの自然利子率の推移。詳細は本文のとおり。
  1. 4須藤・瀧塚（2018）は、短期的なショックや名目硬直性等を捨象した上で、100年間という長期を分析しており、同モデルの実質金利は、ニューケインジアン型モデルの自然利子率と等しいと考えられるため、本稿では、実質金利を自然利子率と読み替えている。
  2. 5須藤・瀧塚（2018）では、21~100歳の家計をモデル化しているため、モデル上の出生率は、実際のデータ上では21歳人口成長率に対応する。

おわりに

本稿では、構造型アプローチを用いてわが国の自然利子率を分析した岡崎・須藤（2018）と須藤・瀧塚（2018）の結果を基に、自然利子率の動向や変動要因、先行きの自然利子率への人口動態要因の影響について整理した。

これら構造型アプローチおよび他の手法によるそれぞれ異なる推計結果を総合的に判断すると、わが国の自然利子率は、1990年代から趨勢的に低下し、最近は概ね0%程度の範囲内にあるとみられる。構造型アプローチによれば、趨勢的な低下の主因は、技術進歩率の変化である。また、1990年代半ば以降の銀行危機時や近年など時期によっては、金融仲介活動の機能度も自然利子率の変動に相応に寄与したとみられる。

自然利子率は、今後もこれらの要因を含む経済構造の変化に大きく依存して推移すると考えられる。わが国の場合、少子高齢化の一段の進展が確実視されている。こうした人口動態の変化は自然利子率の下押し圧力となるが、自然利子率の水準をはっきりと押し下げるものではないとみられる。

参考文献

日本銀行から

本稿の内容と意見は筆者ら個人に属するものであり、日本銀行の公式見解を示すものではありません。